Parallelizing Julia with a
Non-invasive DSL
Hai (Paul) Liu
Intel Labs
June 22, 2017
With Todd Anderson1, Lindsey Kuper1, Ehsan Totoni1, Jan Vitek2, Tatiana Shpeisman1
1Intel Labs 2Northeastern University
Productivity languages are great for prototyping
Matlab, Python, R, …
Safe.
Dynamically typed.
Interactive dev environment.
Thriving eco-system.
But what about performance?
Option 1: re-implement in an HPC language (Fortran/C/C++)
Fast? Maybe.
Low-level, hard to use.
Hard to debug.
Hard to maintain.
Demands skills not possessed by domain experts.
Option 2: Use a high performance library
Bindings to low-level libraries such as OpenBLAS, MKL, …
Good performance.
Easy to use.
Restricted by interface.
Not cache friendly.
Library calls do not compose in parallel.
Option 3: Use a DSL (and its compiler)
High-level abstraction with domain semantics.
Compiled and optimized for performance.
Learning curve.
Hard to debug.
Limited eco-system.
Solution: a non-invasive DSL
Writes like a library.
Runs like a compiler.
Julia: a dynamic language for numerical computing
Matlab-like syntax.
Powerful macros.
Expressive type system.
Performance via LLVM JIT.
K-Means example
# D: number of dimensions
# N: number of points
# C: number of centers
function kmeans(C, iterations, pts)
D,N = size(pts)
centers = rand(D, C)
for l in 1:iterations
dists = [sqrt(sum((pts[:,i]-centers[:,j])^2)) for j in 1:C, i in 1:N]
labels = [indmin(dists[:,i]) for i in 1:N]
centers = [sum(pts[j,labels.==i])/sum(labels.==i) for j in 1:D, i in 1:C]
end
return centers
end
# D: number of dimensions
# N: number of points
# C: number of centers
function kmeans(C, iterations, pts)
D,N = size(pts)
centers = rand(D, C)
for l in 1:iterations
dists = [sqrt(sum((pts[:,i]-centers[:,j])^2)) for j in 1:C, i in 1:N]
labels = [indmin(dists[:,i]) for i in 1:N]
centers = [sum(pts[j,labels.==i])/sum(labels.==i) for j in 1:D, i in 1:C]
end
return centers
end
# D: number of dimensions
# N: number of points
# C: number of centers
function kmeans(C, iterations, pts)
D,N = size(pts)
centers = rand(D, C)
for l in 1:iterations
dists = [sqrt(sum((pts[:,i]-centers[:,j])^2)) for j in 1:C, i in 1:N]
labels = [indmin(dists[:,i]) for i in 1:N]
centers = [sum(pts[j,labels.==i])/sum(labels.==i) for j in 1:D, i in 1:C]
end
return centers
end
# D: number of dimensions
# N: number of points
# C: number of centers
function kmeans(C, iterations, pts)
D,N = size(pts)
centers = rand(D, C)
for l in 1:iterations
dists = [sqrt(sum((pts[:,i]-centers[:,j])^2)) for j in 1:C, i in 1:N]
labels = [indmin(dists[:,i]) for i in 1:N]
centers = [sum(pts[j,labels.==i])/sum(labels.==i) for j in 1:D, i in 1:C]
end
return centers
end
# D: number of dimensions
# N: number of points
# C: number of centers
function kmeans(C, iterations, pts)
D,N = size(pts)
centers = rand(D, C)
for l in 1:iterations
dists = [sqrt(sum((pts[:,i]-centers[:,j])^2)) for j in 1:C, i in 1:N]
labels = [indmin(dists[:,i]) for i in 1:N]
centers = [sum(pts[j,labels.==i])/sum(labels.==i) for j in 1:D, i in 1:C]
end
return centers
end
# D: number of dimensions
# N: number of points
# C: number of centers
function kmeans(C, iterations, pts)
D,N = size(pts)
centers = rand(D, C)
for l in 1:iterations
dists = [sqrt(sum((pts[:,i]-centers[:,j])^2)) for j in 1:C, i in 1:N]
labels = [indmin(dists[:,i]) for i in 1:N]
centers = [sum(pts[j,labels.==i])/sum(labels.==i) for j in 1:D, i in 1:C]
end
return centers
endusing ParallelAccelerator
# D: number of dimensions
# N: number of points
# C: number of centers
@acc function kmeans(C, iterations, pts)
D,N = size(pts)
centers = rand(D, C)
for l in 1:iterations
dists = [sqrt(sum((pts[:,i]-centers[:,j])^2)) for j in 1:C, i in 1:N]
labels = [indmin(dists[:,i]) for i in 1:N]
centers = [sum(pts[j,labels.==i])/sum(labels.==i) for j in 1:D, i in 1:C]
end
return centers
endOn steroids!
ParallelAccelerator
A non-invasive DSL compiler for multi-core.
Written in Julia.
Optimizes a subset of Julia language and library calls.
Compiles to C++ with OpenMP (or LLVM with Julia threads).
What is optimized and parallelized
Array operators/functions.
Comprehension.
Stencil (runStencil).
Parallel for-loop (@par).
Compilation Pipeline

dists = [sqrt(sum((pts[:,i]-centers[:,j])^2)) for j in 1:C, i in 1:N]
dists = [sqrt(sum((pts[:,i]-centers[:,j])^2)) for j in 1:C, i in 1:N]
# Domain IR
select(pts, :, i), select(centers, :, j)
dists = [sqrt(sum((pts[:,i]-centers[:,j])^2)) for j in 1:C, i in 1:N]
# Domain IR
map(-, select(pts, :, i), select(centers, :, j))
dists = [sqrt(sum((pts[:,i]-centers[:,j])^2)) for j in 1:C, i in 1:N]
# Domain IR
map(x->x^2,
map(-, select(pts, :, i), select(centers, :, j)))
dists = [sqrt(sum((pts[:,i]-centers[:,j])^2)) for j in 1:C, i in 1:N]
# Domain IR
reduce(+, 0,
map(x->x^2,
map(-, select(pts, :, i), select(centers, :, j))))
dists = [sqrt(sum((pts[:,i]-centers[:,j])^2)) for j in 1:C, i in 1:N]
# Domain IR
sqrt(reduce(+, 0,
map(x->x^2,
map(-, select(pts, :, i), select(centers, :, j)))))
dists = [sqrt(sum((pts[:,i]-centers[:,j])^2)) for j in 1:C, i in 1:N]
# Domain IR
catesianarray((i, j) ->
sqrt(reduce(+, 0,
map(x->x^2,
map(-, select(pts, :, i), select(centers, :, j))))),
(C, N))
dists = [sqrt(sum((pts[:,i]-centers[:,j])^2)) for j in 1:C, i in 1:N]
# Domain IR
dists = catesianarray((i, j) ->
sqrt(reduce(+, 0,
map(x->x^2,
map(-, select(pts, :, i), select(centers, :, j))))),
(C, N))
dists = [sqrt(sum((pts[:,i]-centers[:,j])^2)) for j in 1:C, i in 1:N]
# Domain IR
dists = catesianarray((i, j) ->
sqrt(reduce(+, 0,
map(x->x^2,
map(-, select(pts, :, i), select(centers, :, j))))),
(C, N))
# Parallel IR (after fusion)
parfor k in 1:D
x = pts[k,i] - centers[k,j]
end
dists = [sqrt(sum((pts[:,i]-centers[:,j])^2)) for j in 1:C, i in 1:N]
# Domain IR
dists = catesianarray((i, j) ->
sqrt(reduce(+, 0,
map(x->x^2,
map(-, select(pts, :, i), select(centers, :, j))))),
(C, N))
# Parallel IR (after fusion)
parfor k in 1:D
x = pts[k,i] - centers[k,j]
y = x^2
end
dists = [sqrt(sum((pts[:,i]-centers[:,j])^2)) for j in 1:C, i in 1:N]
# Domain IR
dists = catesianarray((i, j) ->
sqrt(reduce(+, 0,
map(x->x^2,
map(-, select(pts, :, i), select(centers, :, j))))),
(C, N))
# Parallel IR (after fusion)
s = 0
parfor k in 1:D
x = pts[k,i] - centers[k,j]
s += x^2
end
dists = [sqrt(sum((pts[:,i]-centers[:,j])^2)) for j in 1:C, i in 1:N]
# Domain IR
dists = catesianarray((i, j) ->
sqrt(reduce(+, 0,
map(x->x^2,
map(-, select(pts, :, i), select(centers, :, j))))),
(C, N))
# Parallel IR (after fusion)
s = 0
parfor k in 1:D
x = pts[k,i] - centers[k,j]
s += x^2
end
z = sqrt(s)
dists = [sqrt(sum((pts[:,i]-centers[:,j])^2)) for j in 1:C, i in 1:N]
# Domain IR
dists = catesianarray((i, j) ->
sqrt(reduce(+, 0,
map(x->x^2,
map(-, select(pts, :, i), select(centers, :, j))))),
(C, N))
# Parallel IR (after fusion)
dists = array(float64, C, N)
parfor i in 1:C, j in 1:N
s = 0
parfor k in 1:D
x = pts[k,i] - centers[k,j]
s += x^2
end
dists[i,j] = sqrt(s)
end
Switch-on performance
Same program.
Run in parallel with @acc.
Or run sequentially without.
Optimizations
Size inference, loop fusion, allocation hoisting, SIMD vectorization, …
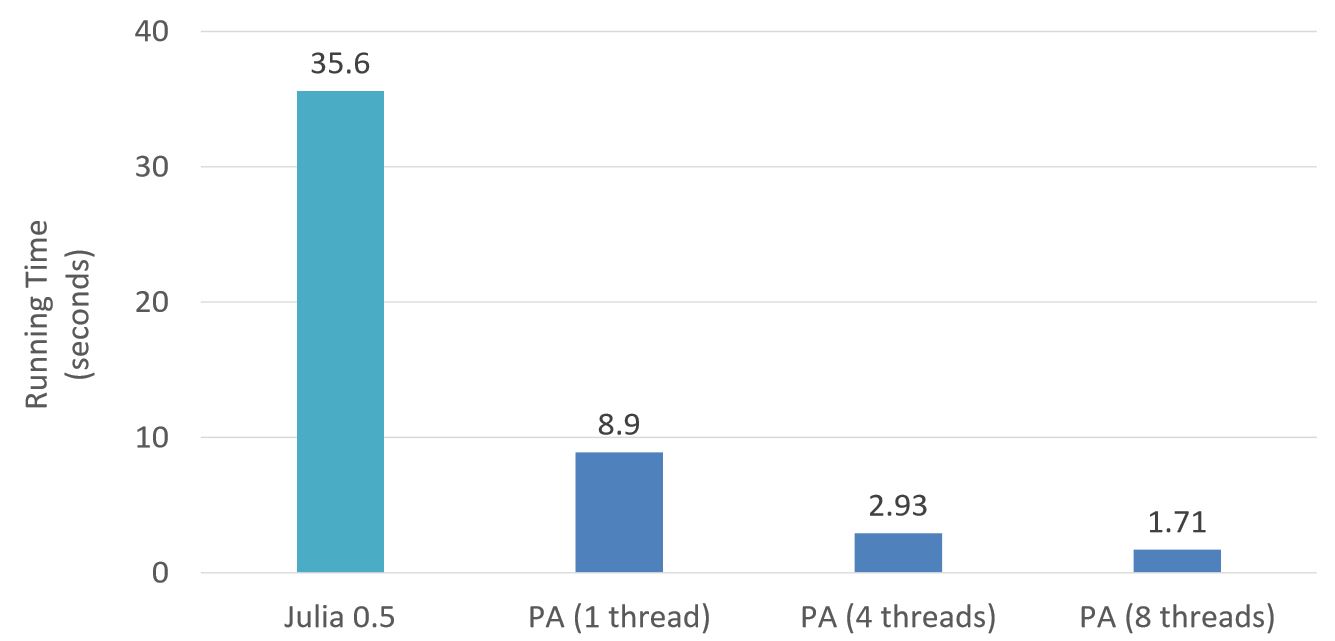
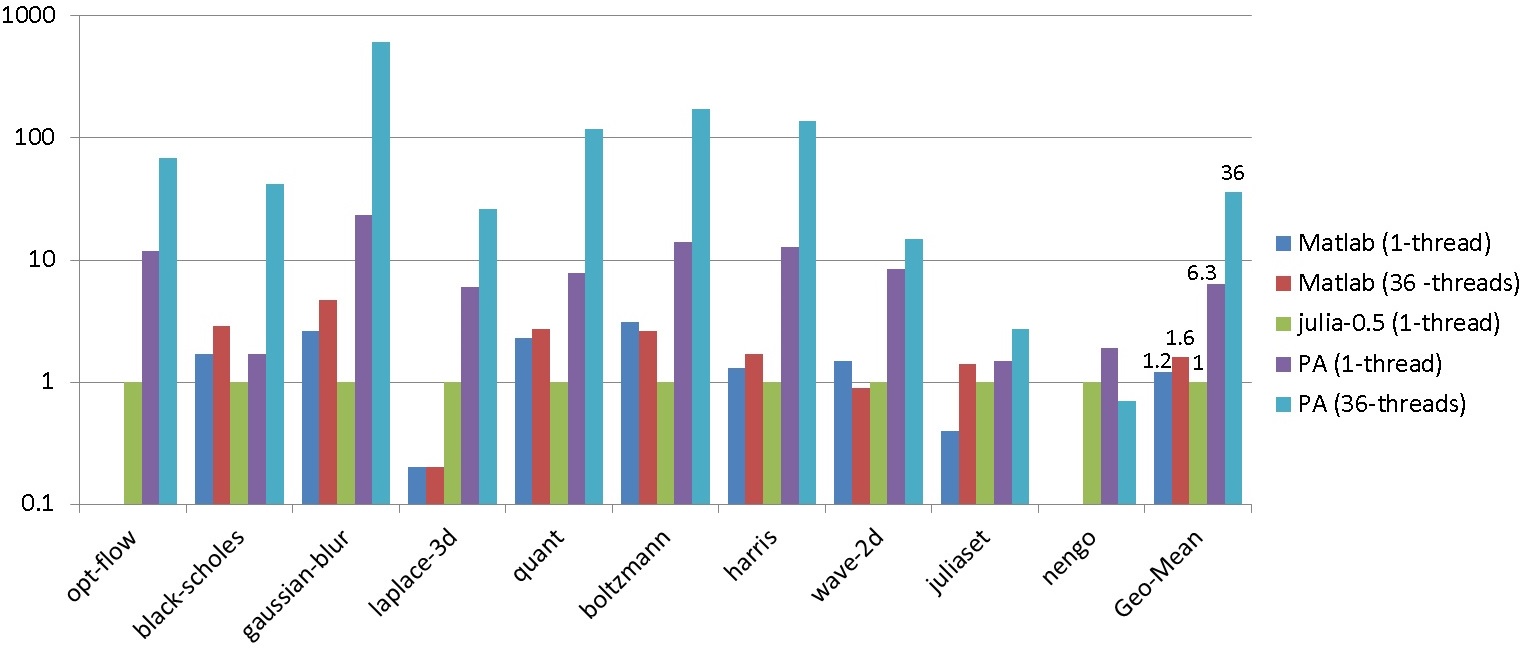
Evaluation (speedups)
Take Away
A non-invasive DSL for parallel computing
Easy to use like a library.
Heavily optimized like a DSL.
Good performance on multi-core.
Flexibility is both a blessing and a curse.
Performance tuning still requires research.
Julia’s macro system and type inference are key enablers.
Thank you!